Сортировка с помощью прямого обмена (пузырьковая сортировка)
Классификация методов сортировки редко бывает осмысленной. Оба разбиравшихся до этого метода можно тоже рассматривать как "обменные" сортировки. В данном же, однако, разделе описан метод, где обмен местами двух элементов представляет собой характернейшую особенность процесса. Изложенный ниже алгоритм прямого обмена основывается на сравнении и смене мест для пары соседних элементов и продолжении этого процесса до тех пор, пока не будут упорядочены все элементы.
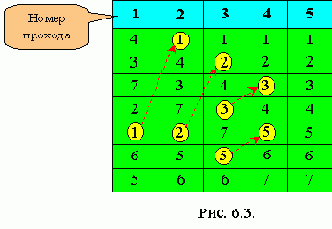
Как и в упоминавшемся методе прямого выбора, мы повторяем проходы по массиву, сдвигая каждый раз наименьший элемент оставшейся последовательности к левому концу массива. Если мы будем рассматривать массивы как вертикальные, а не горизонтальные построения, то элементы можно интерпретировать как пузырьки в чане с водой, причем вес каждого соответствует его ключу. В этом случае при каждом проходе один пузырек как бы поднимается до уровня, соответствующего его весу (см. рис.6.3).
Такой метод широко известен под именем "пузырьковая сортировка". В своем простейшем виде он представлен ниже.
Программы на псевдокоде и Паскале:
| for i = 2 to n
for j = n to i step -1 if a(j) < a(j - 1) then x = a(j - 1) a(j - 1) = a(j) a(j) = x endif next j next i return | for i := 2 to n do
for j := n downto i do if a[j] < a[j - 1]then begin x := a[j - 1]; a[j - 1] := a[j]; a[j] := x; end; end; end; |
В нашем случае получился один проход “вхолостую”. Чтобы лишний раз не переставлять элементы, можно ввести флажок fl, который остается в значении false , если при очередном проходе не будет произведено ни одного обмена. На нижеприведенном алгоритме добавления отмечены курсивом.
fl = true
for i = 2 to n
if fl = false then return
endif
fl = false
for j = n to i step -1
if a(j) < a(j - 1) then
fl = true
x = a(j - 1)
a(j - 1) = a(j)
a(j) = x
endif
next j
next i
return
Улучшением пузырькового метода является шейкерная сортировка, где после каждого прохода меняют направление во внутреннем цикле.
Эффективность алгоритма:
Число сравнений Cmax = n(n-1)/2 , О(n2).
Число перемещений Мmax=3Cmax=3n(n-1)/2, О(n2).
Если массив уже отсортирован и применяется алгоритм с флажком, то достаточно всего одного прохода, и тогда получаем минимальное число сравнений
Cmin = n - 1, О(n),
а перемещения вообще отсутствуют
Сравнительный анализ прямых сортировок показывает, что обменная "сортировка" в классическом виде представляет собой нечто среднее между сортировками с помощью включений и с помощью выбора. Если же в нее внесены приведенные выше усовершенствования, то для достаточно упорядоченных массивов пузырьковая сортировка даже имеет преимущество.
