Сортировка методом прямого включения
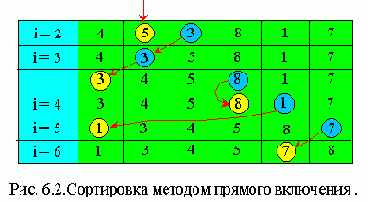
Такой метод широко используется при игре в карты. Элементы мысленно делятся на уже готовую последовательность a1,...,ai-1 и исходную последовательность. При каждом шаге, начиная с i = 2 и увеличивая i каждый раз на единицу, из исхожной последовательности извлекается i-й элемент и перекладывается в готовую последовательность, при этом он вставляется на нужное место.На рис. 6.2 показан в качестве примера процесс сортировки с помощью включения шести случайно выбранных чисел. Алгоритм этой сортировки таков:
for i = 2 to n
x = a(i)
находим место среди а(1)…а(i) для включения х
next i
Для сортировки методом прямого включения пользуются следующими приемами:
| Псевдокод:
Без барьера: for i = 2 to n x = a(i) for j = i - 1 downto 1 if x < a(j ) then a( j + 1) = a(j ) else go to L endif next j L: a( j + 1) = x next i return  С барьером: for i = 2 to n x = a(i) a(0) = x {a(0) - барьер} j = i - 1 while x < a(j ) do a( j +1) = a(j ) j = j - 1 endwhile a( j +1) = x next i return | Паскаль:
Без барьера: for i:= 2 to n do begin x:= a(i); for j:= i - 1downto 1 do if x < a(j ) then a(j +1):= a(j ) else goto 1; end; end; 1: a(j + 1):= x; end; end; С барьером: for i := 2 to n do begin x:= a(i); a(0):= x; {a(0) - барьер} j:= i - 1; while x < a(j ) do begin a(j +1):= a(j ); j:=j - 1; end; a(j +1):= x; end; |
Эффективность алгоритма
Число сравнений ключей Ci при i- м просеивании самое большее равно i-1, самое меньшее - 1; если предположить, что все перестановки из N ключей равновероятны, то среднее число сравнений = i/2. Число же пересылок Mi=Ci+3 (включая барьер). Минимальные оценки встречаются в случае уже упорядоченной исходной последовательности элементов, наихудшие же оценки - когда они первоначально расположены в обратном порядке. В некотором смысле сортировка с помощью включения демонстрирует истинно естественное поведение. Ясно, что приведенный алгоритм описывает процесс устойчивой сортировки: порядок элементов с равными ключами при нем остается неизменным.
Количество сравнений в худшем случае, когда массив отсортирован противоположным образом, Сmax = n(n - 1)/2, т. е. - О (n2). Количество перестановок Mmax = Cmax + 3(n-1), т.е. - О (n2). Если же массив уже отсортирован, то число сравнений и перестановок минимально: Cmin = n-1; Mmin = =3(n-1).
