Поиск с удалением
Удаление узла не должно нарушить упорядоченности дерева. Возможны три варианта:
1) Найденный узел является листом. Тогда он просто удаляется и все.
2) Найденный узел имеет только одного сына. Тогда сын перемещается на место отца.
3) У удаляемого узла два сына. В этом случае нужно найти подходящее звено поддерева, которое можно было бы вставить на место удаляемого. Такое звено всегда существует:
- это либо самый правый элемент левого поддерева (для достижения этого звена необходимо перейти в следующую вершину по левой ветви, а затем переходить в очередные вершины только по правой ветви до тех пор, пока очередная ссылка не будет равна NIL.
- либо самый левый элемент правого поддерева (для достижения этого звена необходимо перейти в следующую вершину по правой ветви, а затем переходить в очередные вершины только по левой ветви до тех пор, пока очередная ссылка не будет равна NIL
Предшественником удаляемого узла называют самый правый узел левого поддерева (для 12 - 11). Преемником - самый левый узел правого поддерева (для 12 - 13).
Будем разрабатывать алгоритм для преемника (рис.5.9).
p - рабочий указатель;
q - отстает от р на один шаг;
v - указывает на приемника удаляемого узла;
t - отстает от v на один шаг;
s - на один шаг впереди v (указывает на левого сына или пустое место).
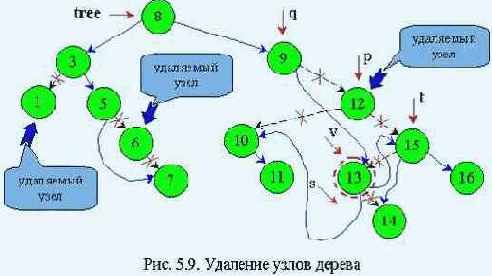
На узел 13 в конечном итоге должен указывать v, а указатель s - на пустое место (как показано на рис. 5.9).
| Псевдокод:
q = nil p = tree while (p <> nil) and (k(p) <> key) do q = p if key < k(p) then p = left(p) else p = right(p) endif endwhile if p = nil then ‘Ключ не найден’ return endif if left(p) = nil then v = right(p) else if right(p) = nil then v = left(p) else ‘У nod(p) - два сына’ ‘Введем два указателя (t отстает от v на 1 ‘шаг, s - опережает) t = p v = right(p) s = left(v) while s <> nil do t = v v = s s = left(v) endwhile if t <> p then ‘v не является сыном p’ left(t) = right(v) right(v) = right(p) endif left(v) = left(p) endif endif if q = nil then ‘p - корень’ tree = v else if p = left(q) then left(q) = v else right(q) = v endif endif freenode(p) return | Паскаль:
q := nil; p := tree; while (p <> nil) and (p^.k <> key) do begin q := p; if key < p^.k then p := p^.left else p := p^.right; end; if p = nil then WriteLn(‘Ключ не найден’); exit; end; if p^.left = nil then v := p^.right else if p^.right = nil then v := p^.left else begin {Введем два указателя (t отстает от v на 1 шаг, s - опережает)} t := p; v := p^.right; s := v^.left; while s <> nil do begin t := v; v := s; s := v^.left; end; if t <> p then begin WriteLn(‘v не является сыном p’); t^.left := v^.right; v^.right := p^.right; end; v^.left := p^.left; end; end; if p = q^.left then q^.left := v else q^.right := v; end; dispose(p); end; |
Контрольные вопросы
1. В чем состоит назначение поиска ?
2. Что такое уникальный ключ ?
3. Какая операция производится в случае отсутствия заданного ключа в списке ?
4. В чем разница между последовательным и индексно-последовательным поиском ?
5. Какой из них более эффективный и почему ?
6. Какие способы переупорядочивания таблицы вы знаете ?
7. Основные отличия метода перестановки в начало от метода транспозиции .
8. Где они будут работать быстрее, в массиве или списке ?
9. В каких списках они работают, упорядоченных или нет ?
10. В чем суть бинарного поиска?
11. Как можно обойти бинарное дерево?
12. Можно ли применять бинарный поиск к массивам ?
13. Если удалить корень в непустом бинарном дереве, какой элемент станет на его место ?
