Очередь
Понятие очереди всем хорошо известно из повседневной жизни. Элементами очереди в общем случае являются заказы на то или иное обслуживание.
В программировании имеется структура данных, которая называется очередью. Эта структура данных используется, например, для моделирования реальных очередей с целью определения их характеристик при данном законе поступления заказов и дисциплине их обслуживания. По своему существу очередь является полустатической структурой- с течением времени и длина очереди, и состав могут изменяться.
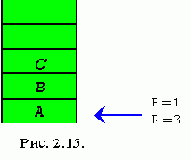
На рис. 2. 13 приведена очередь, содержащая четыре элемента — А, В, С и D. Элемент А расположен в начале очереди, а элемент D — в ее конце. Элементы могут удаляться только из начала очереди, то есть первый помещаемый в очередь элемент удаляется первым. По этой причине очередь часто называют списком, организованным по принципу «первый размещенный первым удаляется» в противоположность принципу стековой организации — «последний размещенный первым удаляется».
Дисциплину обслуживания, в которой заказ, поступивший в очередь первым, выбирается первым для обслуживания (и удаляется из очереди), называется FIFO (First In First Out - Первым пришел, первым ушел). Очередь открыта с обеих сторон.
Таким образом, изъятие компонент происходит из начала очереди, а запись- в конец. В этом случае вводят два указателя: один - на начало очереди, второй- на ее конец.
Реальная очередь создается в памяти ЭВМ в виде одномерного массива с конечным числом элементов, при этом необходимо указать тип элементов очереди, а также необходима переменная в работе с очередью.

Физически очередь занимает сплошную область памяти и элементы следуют друг за другом, как в последовательном списке.
Операции, производимые над очередью:
Для очереди определены три примитивные операции. Операция insert (q,x) помещает элемент х в конец очереди q. Операция remove(q) удаляет элемент из начала очереди q и присваивает его значение переменной х. Третья операция, empty (q), возвращает значение true или false в зависимости от того, является ли данная очередь пустой или нет.
Кроме того. Учитывая то, что полустатическая очередь реализуется на одномерном массиве, необходимо следить за возможностью его переполнения. Сэтой целью вводится опнрация full(q).
Операция insert может быть выполнена всегда, поскольку на количество элементов, которые может содержать очередь, никаких ограничений не накладывается. Операция remove, однако, применима только к непустой очереди, поскольку невозможно удалить элемент из очереди, не содержащей элементов. Результатом попытки удалить элемент из пустой очереди является возникновение исключительной ситуации
потеря значимости. Операция empty, разумеется, выполнима всегда.
Пример реализации очереди в виде одномерного массива на Паскале:
const
MaxQ = ...
type
E = ...
Queue = Array [1..MaxQ] of E;
var
Q: Queue;
F, R: Integer;
{Указатель F указывает на начало очереди. Указатель R указывает на конец очереди. Если очередь пуста, то F = 1, а R = 0 (То есть R < F – условие пустоты очереди).}
Procedure Insert(I: Integer; var Q: Queue);
begin
Inc(R);
Q[R]:=I;
end;
Function Empty(Q: Queue): Boolean;
begin
If R < F then Empty:=True Else Empty:=False;
end;
Procedure Remove(var I: Integer; Q: Queue);
begin
If Not Empty(Q) then
begin
I:=Q[F];
Inc(F);
end;
end;
Пример работы с очередью с использованием стандартных процедур.
MaxQ = 5
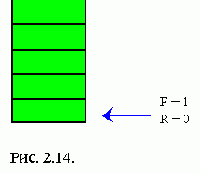
Производим вставку элементов A, B и C в очередь.
Insert(q, A);
Insert(q, B);
Insert(q, C);
Убираем элементы A и B из очереди.
Remove(q);
Remove(q);
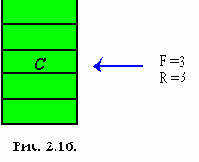
К сожалению, при подобном представлении очереди, возможно возникновение абсурдной ситуации, при которой очередь является пустой, однако новый элемент разместить в ней нельзя (рассмотрите последовательность операций удаления и вставки, приводящую к такой ситуации). Ясно, что реализация очереди при помощи массива является неприемлемой.
Одним из решений возникшей проблемы может быть модификация операции remove таким образом, что при удалении очередного элемента вся очередь смещается к началу массива.
Операция remove (q) может быть в этом случае реализована следующим образом.
X = q[1]
For I =1 to R-1
q[I] =q[I+1]
next I
R =R-1
Переменная F больше не требуется, поскольку первый элемент массива всегда является началом очереди. Пустая очередь представлена очередью, для которой значение R равно нулю.
Однако этот метод весьма непроизводителен. Каждое удаление требует перемещения всех оставшихся в очереди элементов. Если очередь содержит 500 или 1000 элементов, то очевидно, что это весьма неэффективный способ. Далее, операция удаления элемента из очереди логически предполагает манипулирование только с одним элементом, т. е. с тем, который расположен в начале очереди. Реализация данной операции должна отражать именно этот факт, не производя при этом множества дополнительных действий.
Другой способ предполагает рассматривать массив, который содержит очередь в виде замкнутого кольца, а не линейной последовательности, имеющей начало и конец. Это означает, что первый элемент очереди следует сразу же за последним. Это означает, что даже в том случае, если последний элемент занят, новое значение может быть размещено сразу же за ним на месте первого элемента, если этот первый элемент пуст.
Организация кольцевой очереди.
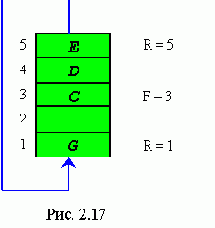
Рассмотрим пример. Предположим, что очередь содержит три элемента - в позициях 3, 4 и 5 пятиэлементного массива. Этот случай, показанный на рис. 2.17. Хотя массив и не заполнен, последний элемент очереди занят.
Если теперь делается попытка поместить в очередь элемент G, то он будет записан в первую позицию массива, как это показано на рис. 2.17. Первый элемент очереди есть Q(3), за которым следуют элементы Q (4), Q(5) и Q(l).
К сожалению, при таком представлении довольно трудно определить, когда очередь пуста. Условие R<F больше не годится для такой проверки, поскольку на рис. 2. 17 показан случай, при котором данное условие выполняется, но очередь при этом не является пустой.
Одним из способов решения этой проблемы является введение соглашения, при котором значение F есть индекс элемента массива, немедленно предшествующего первому элементу очереди, а не индексу самого первого элемента.
В этом случае, поскольку R содержит индекс последнего элемента очереди, условие F = R подразумевает, что очередь пуста.
Отметим, что перед началом работы с очередью, в F и R устанавливается значение последнего индекса массива, а не 0 и 1, поскольку при таком представлении очереди последний элемент массива немедленно предшествует первому элементу. Поскольку R = F, то очередь изначально пуста.
Основные операции с кольцевой очередью:
1. Вставка элемента q в очередь x.
Insert(q,x)
2. Извлечение элемента из очереди x.
Remove(q)
3. Проверка очереди на пустоту.
Empty(q)
Операция empty (q) может быть записана следующим образом:
if F = R
then empty = true
else empty = false
endif
return
Операция remove (q) может быть записана следующим образом:
empty (q)
if empty = true
then print «выборка из пустой очереди»
stop
endif
if F =maxQ
then F =1
else F = F+1
endif
x = q(F)
return
Отметим, что значение F должно быть модифицировано до момента извлечения элемента.
Операция вставки insert (q,x).
Для того чтобы запрограммировать операцию вставки, должна быть проанализирована ситуация, при которой возникает переполнение. Переполнение происходит в том случае, если весь массив уже занят элементами очереди и при этом делается попытка разместить в ней еще один элемент. Рассмотрим, например, очередь на рис. 2. 17. В ней находятся три элемента — С, D и Е, соответственно расположенные в Q (3), Q (4) и Q (5). Поскольку последний элемент в очереди занимает позицию Q (5), значение R равно 5. Так как первый элемент в очереди находится в Q (3), значение F равно 2. На рис. 2. 17 в очередь помещается элемент G, что приводит к соответствующему изменению значения R. Если произвести следующую вставку, то массив становится целиком заполненным, и попытка произвести еще одну вставку приводит к переполнению. Это регистрируется тем фактом, что F = R, а это как раз и указывает на переполнение. Очевидно, что при такой реализации нет возможности сделать различие между пустой и заполненной очередью Разумеется, такая ситуация удовлетворить нас не может
Одно из решений состоит в том, чтобы пожертвовать одним элементом массива и позволить очереди расти до объема на единицу меньшего максимального. Так, если массив из 100 элементов объявлен как очередь, то очередь может содержать до 99 элементов. Попытка разместить в очереди 100-й элемент приведет к переполнению. Подпрограмма insert может быть записана следующим образом:
if R = max(q)
then R = 1
else R = R+1
endif
'проверка на переполнение
if R = F
then print «переполнение очереди»
stop
endif
q (r) =x
return
Проверка на переполнение в подпрограмме insert производится после установления нового значения для R, в то время как проверка на потерю значимости в подпрограмме remove производится сразу же после входа в подпрограмму до момента обновления значения F.
